[算法][纠错][ECC]NAND FLASH ECC校验原理与实现, http://www.dragon-2008.com/circuit/Article/NAND_ECC.htm Options

[猫猫草]

ECC简介
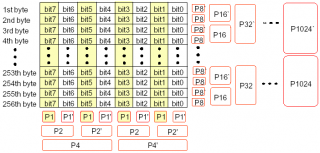
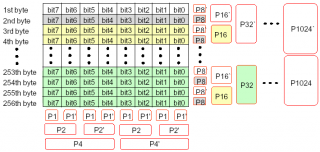
　　由于NAND Flash的工艺不能保证NAND的Memory Array在其生命周期中保持性能的可靠，因此，在NAND的生产中及使用过程中会产生坏块。为了检测数据的可靠性，在应用NAND Flash的系统中一般都会采用一定的坏区管理策略，而管理坏区的前提是能比较可靠的进行坏区检测。
　　如果操作时序和电路稳定性不存在问题的话，NAND Flash出错的时候一般不会造成整个Block或是Page不能读取或是全部出错，而是整个Page（例如512Bytes）中只有一个或几个bit出错。
　　对数据的校验常用的有奇偶校验、CRC校验等，而在NAND Flash处理中，一般使用一种比较专用的校验——ECC。ECC能纠正单比特错误和检测双比特错误，而且计算速度很快，但对1比特以上的错误无法纠正，对2比特以上的错误不保证能检测。

ECC原理
　　ECC一般每256字节原始数据生成3字节ECC校验数据，这三字节共24比特分成两部分：6比特的列校验和16比特的行校验，多余的两个比特置1，如下图所示：

　　ECC的列校验和生成规则如下图所示：


　　用数学表达式表示为：
　　　　P4=D7(+)D6(+)D5(+)D4　　P4`=D3(+)D2(+)D1(+)D0
　　　　P2=D7(+)D6(+)D3(+)D2　　P2`=D5(+)D4(+)D1(+)D0
　　　　P1=D7(+)D5(+)D3(+)D1　　P1`=D6(+)D4(+)D2(+)D0
　　这里(+)表示“位异或”操作
　　
　　ECC的行校验和生成规则如下图所示：

　　用数学表达式表示为：
　　　　P8 = bit7(+)bit6(+)bit5(+)bit4(+)bit3(+)bit2(+)bit1(+)bit0(+)P8
　　　　……………………………………………………………………………………
　　这里(+)同样表示“位异或”操作
　
　　当往NAND Flash的page中写入数据的时候，每256字节我们生成一个ECC校验和，称之为原ECC校验和，保存到PAGE的OOB（out-of-band）数据区中。
　　当从NAND Flash中读取数据的时候，每256字节我们生成一个ECC校验和，称之为新ECC校验和。
　　校验的时候，根据上述ECC生成原理不难推断：将从OOB区中读出的原ECC校验和新ECC校验和按位异或，若结果为0，则表示不存在错（或是出现了 ECC无法检测的错误）；若3个字节异或结果中存在11个比特位为1，表示存在一个比特错误，且可纠正；若3个字节异或结果中只存在1个比特位为1，表示 OOB区出错；其他情况均表示出现了无法纠正的错误。

ECC算法的实现

代码

static const u_char nand_ecc_precalc_table[] =
  {
    0x00, 0x55, 0x56, 0x03, 0x59, 0x0c, 0x0f, 0x5a, 0x5a, 0x0f, 0x0c, 0x59, 0x03, 0x56, 0x55, 0x00,
    0x65, 0x30, 0x33, 0x66, 0x3c, 0x69, 0x6a, 0x3f, 0x3f, 0x6a, 0x69, 0x3c, 0x66, 0x33, 0x30, 0x65,
    0x66, 0x33, 0x30, 0x65, 0x3f, 0x6a, 0x69, 0x3c, 0x3c, 0x69, 0x6a, 0x3f, 0x65, 0x30, 0x33, 0x66,
    0x03, 0x56, 0x55, 0x00, 0x5a, 0x0f, 0x0c, 0x59, 0x59, 0x0c, 0x0f, 0x5a, 0x00, 0x55, 0x56, 0x03,
    0x69, 0x3c, 0x3f, 0x6a, 0x30, 0x65, 0x66, 0x33, 0x33, 0x66, 0x65, 0x30, 0x6a, 0x3f, 0x3c, 0x69,
    0x0c, 0x59, 0x5a, 0x0f, 0x55, 0x00, 0x03, 0x56, 0x56, 0x03, 0x00, 0x55, 0x0f, 0x5a, 0x59, 0x0c,
    0x0f, 0x5a, 0x59, 0x0c, 0x56, 0x03, 0x00, 0x55, 0x55, 0x00, 0x03, 0x56, 0x0c, 0x59, 0x5a, 0x0f,
    0x6a, 0x3f, 0x3c, 0x69, 0x33, 0x66, 0x65, 0x30, 0x30, 0x65, 0x66, 0x33, 0x69, 0x3c, 0x3f, 0x6a,
    0x6a, 0x3f, 0x3c, 0x69, 0x33, 0x66, 0x65, 0x30, 0x30, 0x65, 0x66, 0x33, 0x69, 0x3c, 0x3f, 0x6a,
    0x0f, 0x5a, 0x59, 0x0c, 0x56, 0x03, 0x00, 0x55, 0x55, 0x00, 0x03, 0x56, 0x0c, 0x59, 0x5a, 0x0f,
    0x0c, 0x59, 0x5a, 0x0f, 0x55, 0x00, 0x03, 0x56, 0x56, 0x03, 0x00, 0x55, 0x0f, 0x5a, 0x59, 0x0c,
    0x69, 0x3c, 0x3f, 0x6a, 0x30, 0x65, 0x66, 0x33, 0x33, 0x66, 0x65, 0x30, 0x6a, 0x3f, 0x3c, 0x69,
    0x03, 0x56, 0x55, 0x00, 0x5a, 0x0f, 0x0c, 0x59, 0x59, 0x0c, 0x0f, 0x5a, 0x00, 0x55, 0x56, 0x03,
    0x66, 0x33, 0x30, 0x65, 0x3f, 0x6a, 0x69, 0x3c, 0x3c, 0x69, 0x6a, 0x3f, 0x65, 0x30, 0x33, 0x66,
    0x65, 0x30, 0x33, 0x66, 0x3c, 0x69, 0x6a, 0x3f, 0x3f, 0x6a, 0x69, 0x3c, 0x66, 0x33, 0x30, 0x65,
    0x00, 0x55, 0x56, 0x03, 0x59, 0x0c, 0x0f, 0x5a, 0x5a, 0x0f, 0x0c, 0x59, 0x03, 0x56, 0x55, 0x00
  };

  // Creates non-inverted ECC code from line parity
  static void nand_trans_result(u_char reg2, u_char reg3,u_char *ecc_code)
  {
    u_char a, b, i, tmp1, tmp2;

    /* Initialize variables */
    a = b = 0x80;
    tmp1 = tmp2 = 0;

    /* Calculate first ECC byte */
    for (i = 0; i < 4; i++)
    {
      if (reg3 & a)    /* LP15,13,11,9 --> ecc_code[0] */
        tmp1 |= b;
      b >>= 1;
      if (reg2 & a)    /* LP14,12,10,8 --> ecc_code[0] */
        tmp1 |= b;
      b >>= 1;
      a >>= 1;
    }

    /* Calculate second ECC byte */
    b = 0x80;
    for (i = 0; i < 4; i++)
    {
      if (reg3 & a)    /* LP7,5,3,1 --> ecc_code[1] */
        tmp2 |= b;
      b >>= 1;
      if (reg2 & a)    /* LP6,4,2,0 --> ecc_code[1] */
        tmp2 |= b;
      b >>= 1;
      a >>= 1;
    }

    /* Store two of the ECC bytes */
    ecc_code[0] = tmp1;
    ecc_code[1] = tmp2;
  }

  // Calculate 3 byte ECC code for 256 byte block
  void nand_calculate_ecc (const u_char *dat, u_char *ecc_code)
  {
    u_char idx, reg1, reg2, reg3;
    int j;

    /* Initialize variables */
    reg1 = reg2 = reg3 = 0;
    ecc_code[0] = ecc_code[1] = ecc_code[2] = 0;

    /* Build up column parity */
    for(j = 0; j < 256; j++)
    {

      /* Get CP0 - CP5 from table */
      idx = nand_ecc_precalc_table[dat[j]];
      reg1 ^= (idx & 0x3f);

      /* All bit XOR = 1 ? */
      if (idx & 0x40) {
        reg3 ^= (u_char) j;
        reg2 ^= ~((u_char) j);
      }
    }

    /* Create non-inverted ECC code from line parity */
    nand_trans_result(reg2, reg3, ecc_code);

    /* Calculate final ECC code */
    ecc_code[0] = ~ecc_code[0];
    ecc_code[1] = ~ecc_code[1];
    ecc_code[2] = ((~reg1) << 2) | 0x03;
  }

  // Detect and correct a 1 bit error for 256 byte block
  int nand_correct_data (u_char *dat, u_char *read_ecc, u_char *calc_ecc)
  {
    u_char a, b, c, d1, d2, d3, add, bit, i;

    /* Do error detection */
    d1 = calc_ecc[0] ^ read_ecc[0];
    d2 = calc_ecc[1] ^ read_ecc[1];
    d3 = calc_ecc[2] ^ read_ecc[2];

    if ((d1 | d2 | d3) == 0)
    {
      /* No errors */
      return 0;
    }
    else
    {
      a = (d1 ^ (d1 >> 1)) & 0x55;
      b = (d2 ^ (d2 >> 1)) & 0x55;
      c = (d3 ^ (d3 >> 1)) & 0x54;

      /* Found and will correct single bit error in the data */
      if ((a == 0x55) && (b == 0x55) && (c == 0x54))
      {
        c = 0x80;
        add = 0;
        a = 0x80;
        for (i=0; i<4; i++)
        {
          if (d1 & c)
            add |= a;
          c >>= 2;
          a >>= 1;
        }
        c = 0x80;
        for (i=0; i<4; i++)
        {
          if (d2 & c)
            add |= a;
          c >>= 2;
          a >>= 1;
        }
        bit = 0;
        b = 0x04;
        c = 0x80;
        for (i=0; i<3; i++)
        {
          if (d3 & c)
            bit |= b;
          c >>= 2;
          b >>= 1;
        }
        b = 0x01;
        a = dat[add];
        a ^= (b << bit);
        dat[add] = a;
        return 1;
      }
      else
      {
        i = 0;
        while (d1)
        {
          if (d1 & 0x01)
            ++i;
          d1 >>= 1;
        }
        while (d2)
        {
          if (d2 & 0x01)
            ++i;
          d2 >>= 1;
        }
        while (d3)
        {
          if (d3 & 0x01)
            ++i;
          d3 >>= 1;
        }
        if (i == 1)
        {
          /* ECC Code Error Correction */
          read_ecc[0] = calc_ecc[0];
          read_ecc[1] = calc_ecc[1];
          read_ecc[2] = calc_ecc[2];
          return 2;
        }
        else
        {
          /* Uncorrectable Error */
          return -1;
        }
      }
    }

    /* Should never happen */
    return -1;
  }

[猫猫草]

　　在上文的《NAND FLASH ECC校验原理与实现》中贴出了ECC算法源程序，在ECC算法源程序中有个nand_ecc_precalc_table，用于快速生成ECC校验和，该表实际上是按照《NAND FLASH ECC校验原理与实现》表中的ECC原理生成的，理解了ECC校验和生成原理，实际上生成该表也就不存在任何困难了。下面是生成该表的源程序：

代码

#define   BIT0(x)   ((x)&0x01)
#define   BIT1(x)   (((x)&0x02)>>1)
#define   BIT2(x)   (((x)&0x04)>>2)
#define   BIT3(x)   (((x)&0x08)>>3)
#define   BIT4(x)   (((x)&0x10)>>4)
#define   BIT5(x)   (((x)&0x20)>>5)
#define   BIT6(x)   (((x)&0x40)>>6)
#define   BIT7(x)   (((x)&0x80)>>7)

void MakeEccTable()
{
  int i,m;
  BYTE xData;
  m=0;
  for(i=0;i<256;i++)
  {
    xData=0;
    if(BIT0(i)^BIT2(i)^BIT4(i)^BIT6(i)) xData|=0x01;
    if(BIT1(i)^BIT3(i)^BIT5(i)^BIT7(i)) xData|=0x02;

    if(BIT0(i)^BIT1(i)^BIT4(i)^BIT5(i)) xData|=0x04;
    if(BIT2(i)^BIT3(i)^BIT6(i)^BIT7(i)) xData|=0x08;

    if(BIT0(i)^BIT1(i)^BIT2(i)^BIT3(i)) xData|=0x10;
    if(BIT4(i)^BIT5(i)^BIT6(i)^BIT7(i)) xData|=0x20;

    if(BIT0(i)^BIT1(i)^BIT2(i)^BIT3(i)^BIT4(i)^BIT5(i)^BIT6(i)^BIT7(i))
      xData|=0x40;
    if(m==15)
    {
      TRACE("0x%02X,\n",xData);
      m=0;
    }
    else
    {
      TRACE("0x%02X,",xData);
      m++;
    }
  }
}